一、GNSS定位原理

1、GNSS基本概念

    全球卫星导航系统（GNSS：Global Navigation Satellite System）是一种以卫星为基础的无线电导航系统，系统可提供时间/空间基准和所有与位置信息相关的实时动态信息，又称天基系统。GNSS是否就是GPS？答案是否定的，GNSS包含了多个国家不同的星座系统，主要有美国的GPS系统，欧盟的伽利略系统，俄罗斯的GLONASS系统，中国的北斗系统等另外还有其他的些区域定位系统，如日本QZSS等。

图1 四个主要卫星星座

    每个GNSS星座都是由空间星座部分、地面控制部分以及用户设备部分组成，空间部分提供我们定位所需要的各种信息包括星历（卫星轨道参数等信息）、发射测距信号等；地面控制部分的主要作用是根据监控到的GNSS观测数据，计算出卫星的星历和卫星钟的改造参数，并反馈给卫星，同时可以对卫星进行控制以及发布指令等；用户设备通过接收卫星信号并进行一定的解算，可以获得自身的位置和时间等信息。

2、GNSS定位基本原理

    GNSS定位的基本原理是基于测距，即根据测量得到的卫星与用户设备之间的距离，计算用户自身的位置。我们可以通过哪些信息来计算卫星与用户之间的距离？已知距离信息后需要与哪些信息结合才能够计算出用户自身的位置？

    首先分析如何获取卫星与用户之间的距离，接收机（即用户设备，后续直接称为接收机）一般可以获取到两类距离测量信息，一类是伪距测量，一类是载波相位测量，下面分别说明。接收机可以根据一定的方法接收到卫星发射的信号同时记录当前接收机的时间，卫星发射时间是已知的，因此可以获得信号在空间中传播的时间，由于信号传播速度为光速，因此测量得到的距离为pr称为伪距，即pr不是真实的距离，有一定的误差。

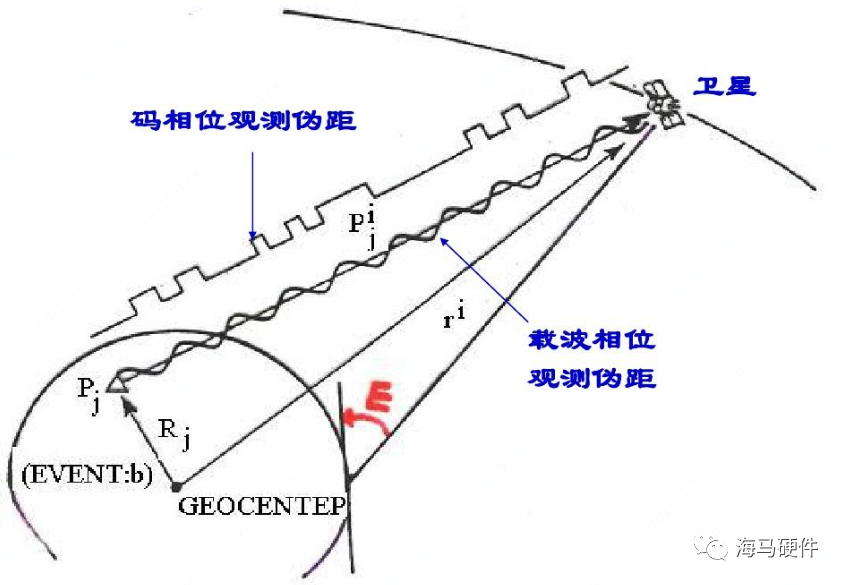
图2 伪距测量

    另外一种距离信息是载波相位测距，载波相位测距不是基于信号空间传播时间完成测量，而是利用了电磁波的相位周期性完成测量；由于GNSS信号是电磁波，相位具有周期性，因此真实的相位应该是N个整周+一个非整周相位，非整周部分可以通过锁相环精确获得，而整周部分N不确定，需要通过其他手段确定，即Cp=(N+γ)*入，其中N为整周，γ一般是未知的，为非整周部分，λ为信号波长。

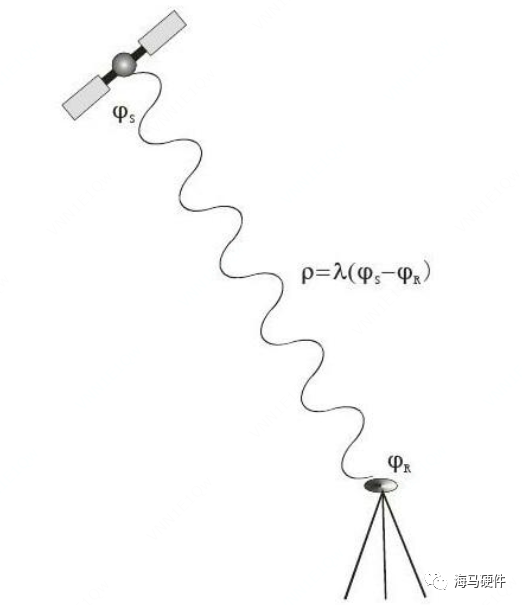
图3 载波相位测距

    载波相位测距与伪距有何区别？主要区别是精度不同，伪距精度一般是~1m，当载波相位整周模糊度固定正确时，精度为~0.001m，因此基于伪距定位精度一般是米级，根据载波相位定位度可以达到cm级。

    我们获取到卫星到接收机的距离时，需要结合哪些信息计算接收机的位置呢？其实我们还有另外一个信息。星历信息，根据星历信息我们可以获取到卫星在各时刻的位詈及速度，结合卫星位置以及卫星与接收机之间的距离，通过最小二乘法或者扩展卡尔曼滤波等方法可以确定接收机的位置。

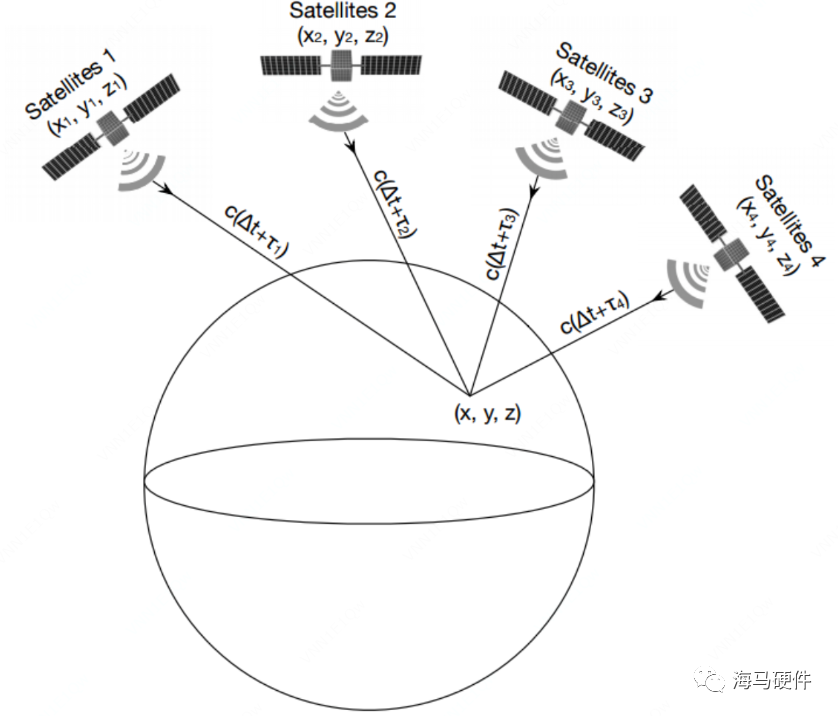
图4 GNSS定位基本原理

3、GNSS定位难点

    如第2节所述，可以很简单的计算出接收机的位置GNSS定位真的这么简单吗？我们详细看一下伪距测量以及载波测量有哪些误差源：①GNSS时钟与接收机不同步；②不同GNSS之间时钟也不同步；③接收机时钟一般存在漂移；④GNSS信号在传幡过程中；会经过大气层和对流层，存在信号反射和折射，因此实际测距或者相位不是真实的距离；⑤接收机与卫星之间可能存在多路径效应，致接收到的信号不是直达信号；⑥在很多地方只能收到极少数卫星无法满足定位需求；⑦部分地方GNSS信号完全被遮挡，无法完成定位。以上只列出了部分误差源，实际情况可能会更复杂具体分类如下：

    与卫星有关的误差：卫星轨误差，卫星钟差；

    与传幡途径有关的误差：电离层延迟，对流层延迟，多路径效应

    与接收设备有关的误差：接收机天线相位中心的偏移和变化，接收机钟差等；

    下图以示意图的方式列出了各误差源：

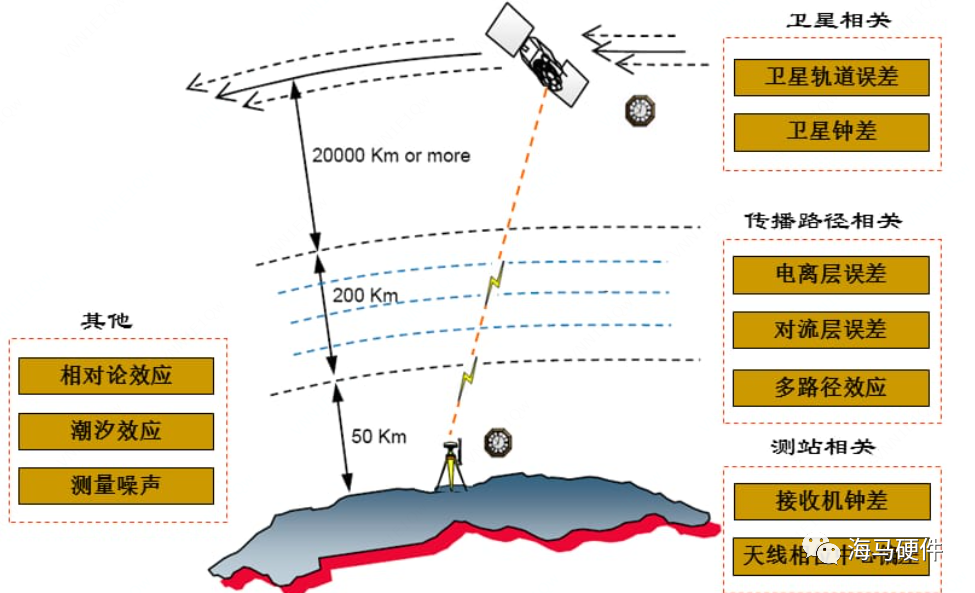
图5 传播过程中测距误差

4、GNSS定位消除误差方法

    消除上述误差一般有如下2种思路：①模型改正法：对误差进行建模估计并补偿；②求差法：通过差分将特定的误差、消除或减弱，根据如何消除这些误差源，实时GNSS定位可以简单分为单点定位、以及RTK定位。

    单点定位直接根据测量得到的伪距信息完成定位，定位过程中对接收机钟差进行建模，部分算法会对电离层和对流层进行建模，计算中采用广播星历精度较低，最终定位精度一般是米级。

    PPP是精密单点定位，是采用精密星历并对接收机和卫星的钟差、时钟漂移、电离层，对流层进行建模，从而实现较高精度定位，PPP定位度可达10cm，但是一般收敛时间较慢，需要30min以上。

    RTK是实时动态定位，除了利用接收机收到信息，还用了差分基站的信息。差分站是一个位置精确已知的高精度接收机，可以接收到与用户接收机比较类似的GNSS信息，差分站接收到GNSS信号后，通过网络传输给用户接收机，用户接收机通过对自身接收的信号与差分站接收到的各信息作差，可以完全消除钟差，卫星轨道等参数影响，也可以削弱电离层和对流层的影响，为何是削弱而不是消除呢？因为此处我们假设卫星到用户接收机的传幡路径中电离层与对流层特征，与卫星到差分站接收机的传播路径中电离层和对流层特征一致，但是在实际场景中，二者不一致，但是比较接近，因此可以削弱电离层与对流层的影响。

    差分定位意图如下：包括站间差分、星间差分以及历元间差分。

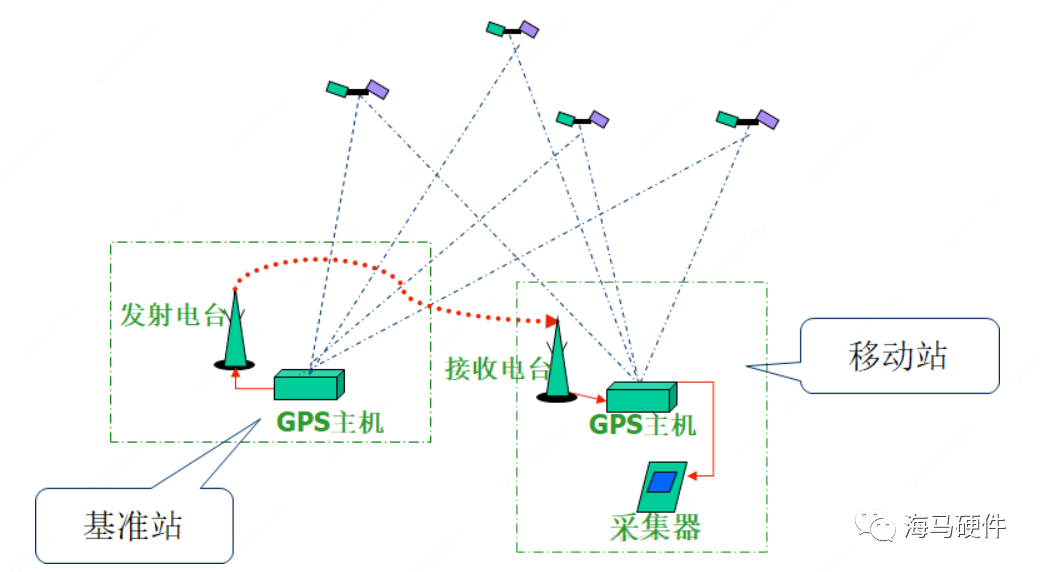
图6 差分定位示意图

    差分定位优点：①消除或减弱一些具有系统性误差的影响；②减少平差计算中未知数的个数。差分定位缺点：①原始独立观测量通过求差将引起差分量之间的相关性；②平差计算中，差分法将使观测方程数明显减少。

5、RTK算法基本原理

    RTK算法是前最常用的GNSS高度定位技术，在开阔场景下，定位度达cm级，且在几秒内就可以完成。

    上节我们介绍了测量误差的修正，当误差修正后我们可以采用修正后的距离测量信息，计算定位结果，高精度定位必须采用载波相位进行定位，但是载波相位存在整周模糊度问题，即必须精确已知整周模糊度才能够获取精确的定位结果，因此RTK算法的核心是整周模糊度固定。

    理论上，整周模糊度N必须是整数但是我们根据最小二乘法或者卡尔曼滤波估计得到的N不是整数，而是实数，如何根据实数获取到整数呢？最基本的方法是搜索即历实数N附近的所有整数，评估定位误差选取误差最小的整数组合即为真实的整周N。由于测量信息中存在载波相位和伪距，二者量测精度差异较大，导致整周模糊度搜索空间巨大，复杂度高，因此我们可以通过数据转换，消除各参数之间的相关性，缩小搜索空间，从而提升算法效率，常用的方法有lambda等。如下图所示：参数变换前后，搜索空间明显减小。

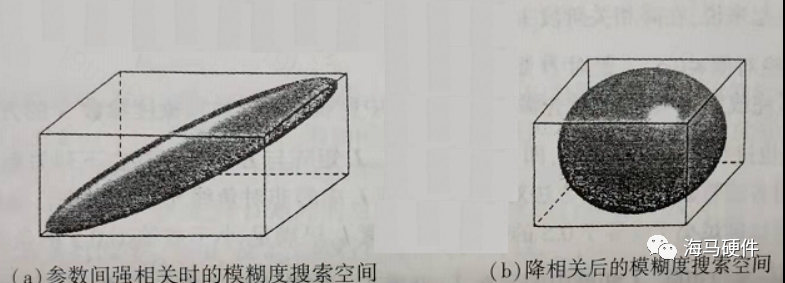
图7 参数空间变换前后搜索空间对比

二、RTK算法缺点及改进方法

    RTK定位在较为开阔环境下定位可达厘米级性能满足高定位要求，但是在复杂环境下定位性能无法保证，因此无法通过单独依靠RTK完成全场景高精度，我们必须通过其他手段来提升定位精度，主要有以下几个方案：1、通过大量历史数据分析，直接优化RTK算法；2、通过结合惯性传感器，利用组合导航的优势提升定位性能；3、采用其他短离高度定位的方式，比如蓝牙定位以及NFC定位等。

三、成果应用及意义

   高精度定位技术是一种非常精密、复杂的精确导航技术。在交通运输、测量测绘、无人机定位、自动驾驶、共享两轮车等领域中具有广泛的应用，它已经成为现代社会中不可或缺的一部分。